Tính chất tâm của đường tròn ngoại tiếp tam giác vuông, cân, đều

Bạn đã biết tâm của đường tròn ngoại tiếp tam giác cân được xác định như thế nào? Trong bài viết hôm nay mình sẽ chia sẻ với các bạn tính chất và cách xác định tâm của đường tròn ngoại tiếp tam giác vuông, cân, đều một cách chi tiết, cụ thể nhất và có bài tập ví dụ nhé.

 

1. Đường tròn ngoại tiếp tam giác

 

Theo định nghĩa, đường tròn ngoại tiếp của tam giác là đường tròn đi qua các đi qua tất cả các đỉnh của tam giác đó và tâm của đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác đó.

 

 

 

Hình ảnh minh họa đường  tròn ngoại tiếp tam giác

 

2. Tâm của đường tròn ngoại tiếp tam giác vuông, cân, đều

Giao của 3 đường trung trực trong tam giác là tâm đường tròn ngoại tiếp (hoặc có thể là 2 đường trung trực).

 

Tính chất đường tròn ngoại tiếp tam giác vuông, cân, đều đó là:

 

•  Mỗi tam giác chỉ có 1 đường tròn ngoại tiếp.

•  

•  Tâm của đường tròn ngoại tiếp tam giác là giao điểm giữa 3 đường trung trực của tam giác. Do vậy tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền. Đối với tam giác cân và tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng với nhau là giao điểm giữa 3 đường trung trực của tam giác

 

3. Cách tính bán kính tâm đường tròn ngoại tiếp tam giác

Các công thức tính bán kính đường tròn ngoại tiếp tam giác:

 

• Công thức tính bán kính đường tròn ngoại tiếp tam giác: R = (a x b x c) : 4S.

•  

• Công thức tính bán kính đường tròn ngoại tiếp của góc A:

 

 

• Công thức tính bán kính đường tròn ngoại tiếp của góc B:

 

 

• Công thức tính bán kính đường tròn ngoại tiếp của góc C:

 

 

Trong đó:

• r: Bán kính đường tròn ngoại tiếp tam giác

•  

• S: Diện tích tam giác.

•  

• a, b, c: Độ dài các cạnh của hình tam giác.

•  

• A, B, C: Các góc của hình tam giác.

 

Các cách tính bán kính tâm đường tròn ngoại tiếp tam giác:

 

Sử dụng định lí sin trong tam giác

Cách đầu tiên chính là sử dụng định lí sin trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác.

 

Ví dụ: Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:

 

 

Trong đó có:

• R: Bán kính đường tròn ngoại tiếp tam giác

•  

• a, b, c: Độ dài các cạnh của hình tam giác.

•  

• A, B, C: Các góc của hình tam giác.

Sử dụng diện tích tam giác

Bên cạnh cách dùng định lý sin, chúng ta cũng có thể sử dụng diện tích trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác:

 

 

Trong đó có:

• R: Bán kính đường tròn ngoại tiếp tam giác.

•  

• S: Diện tích tam giác.

•  

• a, b, c: Độ dài các cạnh của hình tam giác.

•  

• A, B, C: Các góc của hình tam giác.

Sử dụng trong hệ tọa độ

Ngoài ra, tính bán kính đường tròn khi sử dụng trong hệ tọa độ cũng là một cách được rất nhiều người ưa chuộng. Sau đây là các bước cơ bản để tính bán kính:

 

• Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC.

•  

• Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có).

•  

• Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm: R=OA=OB=OC.

Sử dụng tam giác vuông

Sử dụng tam giác vuông để tính bán kính có lẽ là cách cơ bản nhất. Tâm của đường tròn ngoại tiếp trong tam giác vuông là trung điểm của cạnh huyền.

 

Do vậy, bán kính đường tròn ngoại tiếp tam giác vuông là bằng nửa độ dài của cạnh huyền đó.

 

 

Bài tập ví dụ về bán kính đường tròn ngoại tiếp tam giác

 

Bài tập 1: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?

 

 

Áp dụng định lý Pytago, ta có:

 

PQ = 1/2 MP

 

=> NQ = QM = QP = 5cm

 

Gọi D là trung điểm MP.

 

=> ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP

 

=> Q là tâm đường tròn ngoại tiếp ∆MNP

 

=> Đường tròn ngoại tiếp ∆MNP là trung điểm Q của cạnh huyền và bán kính đường tròn ngoại tiếp MNP là R = MQ = 5cm

 

 

Bài tập 2: Cho tam giác ABC có góc B bằng 45° và AC = 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

 

Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.

 

Ta có: b = AC = 4

 

Áp dụng định lý sin trong tam giác ABC ta có:

 

 

 

 

Bài tập 3: Cho tam giác MNP đều với cạnh bằng 12cm. Xác định tâm và bán kính đường tròn ngoại tiếp ∆MNP?

 

 

 

 

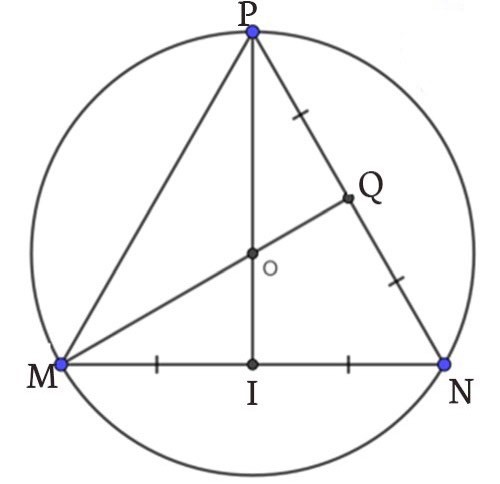
Gọi Q, I lần lượt là trung điểm của cạnh NP, MN và MQ giao với PI tại O.

 

Vì ∆MNP đều nên đường trung tuyến cũng là đường cao, đường phân giác, đường trung trực của tam giác.

 

=> O là tâm của đường tròn ngoại tiếp.

 

=> ∆MNP có PI là đường trung tuyến nên PI cũng là đường cao.

 

Từ đó áp dụng định lý Pytago:

 

PI² = MP² – MI² = 122 – 62 = 108 (cm).

 

=> PI = 6√3cm.

 

Bởi O là trọng tâm của ∆MNP nên:

 

PO = 2/3 PI = 2/3 x 6√3 = 4√3 (cm).

 

 

Trên đây là một số chia sẻ của mình về tính chất tâm của đường tròn ngoại tiếp tam giác cân, vuông, đều và cách tính bán kính đường tròn ngoại tiếp. Cảm ơn các bạn đã theo dõi bài viết nhé.